树

树是一种十分重要的数据结构。树被描述为一种分层数据抽象模型，常用来描述数据间的层级关系和组织结构。树也是一种非顺序的数据结构。下图展示了树的定义：

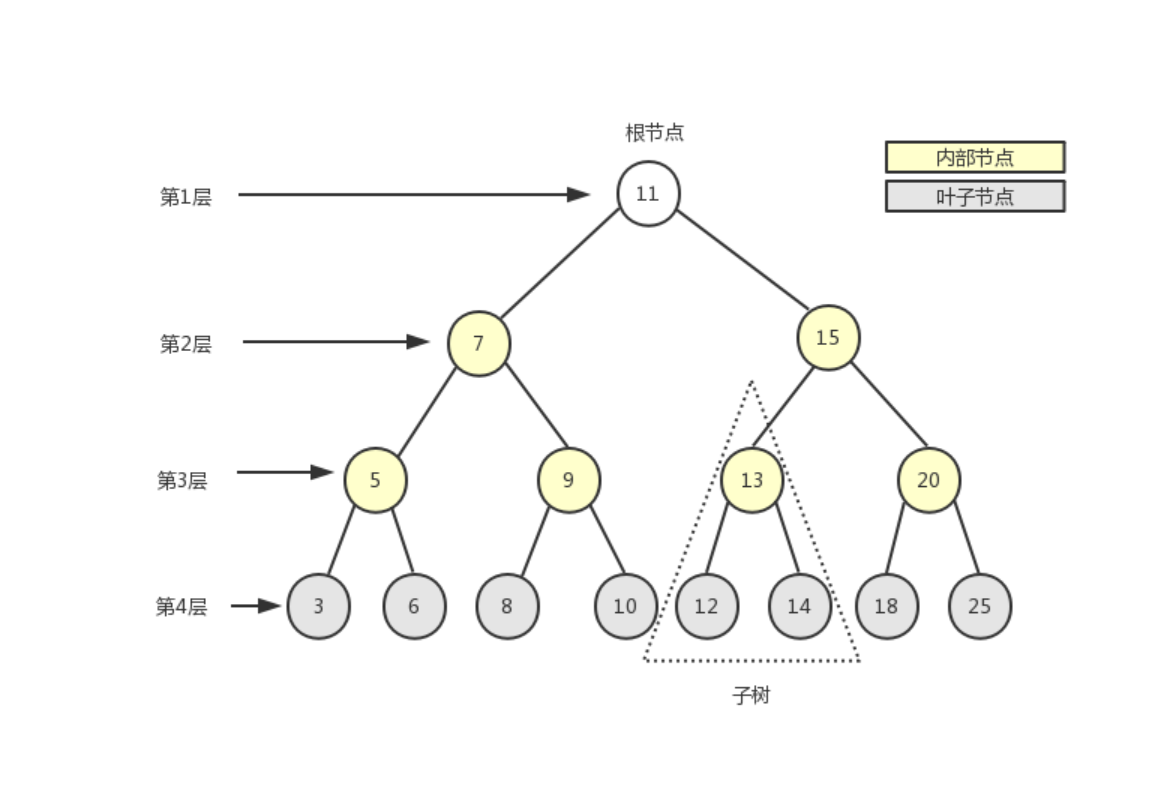
如上图所示，一棵完整的树包含一个位于树顶部的节点，称之为根节点（11），它没有父节点。

树中的每一个元素都叫做一个节点，节点分为内部节点（图中显示为黄色的节点）和外部节点（图中显示为灰色的节点），至少有一个子节点的节点称为内部节点，没有子元素的节点称为外部节点或叶子节点。

一个节点可以有祖先（根节点除外）和后代。子树由节点本身和它的后代组成，如上图中三角虚框中的部分就是一棵子树。节点拥有的子树的个数称之为节点的度，如上图中除叶子节点的度为0外，其余节点的度都为2。

从根节点开始，根为第1层，第一级子节点为第2层，第二级子节点为第3层，以此类推。树的高度（深度）由树中节点的最大层级决定（上图中树的高度为4）。

在一棵树中，具有相同父节点的一组节点称为兄弟节点，如上图中的3和6、5和9等都是兄弟节点。

二叉树

二叉树中的节点最多只能有两个子节点，一个是左子节点，一个是右子节点。左右子节点的顺序不能颠倒。因此，二叉树中不存在度大于2的节点。

二叉搜索树（BST——Binary Search Tree）是二叉树的一种，它规定在左子节点上存储小（比父节点）的值，在右子节点上（比父节点）存储大（或等于）的值。上图就是一个二叉搜索树。

下面我们重点来看一下二叉搜索树的实现。

二叉树的实现

节点结构

为了方便清晰我们分别用 left 表示左节点， right 表示右节点

left 左子节点
el 节点元素
right 右子节点

    class Node {
        constructor(el) {
            this.left = null;   // 左节点
            this.el = el;
            this.right = null   // 右节点
        }
    }

树结构

插入节点
查找节点
中序遍历所有节点
先序遍历所有节点
后序遍历所有节点
最小节点
最大节点
移除节点

class BinarySearchTree {
    constructor () {
        this.root = null;
    }

    // 向树中插入一个节点
    insert (key) {}

    // 在树中查找一个节点
    search (key) {}

    // 通过中序遍历方式遍历树中的所有节点
    inOrderTraverse () {}

    // 通过先序遍历方式遍历树中的所有节点
    preOrderTraverse () {}

    // 通过后序遍历方式遍历树中的所有节点
    postOrderTraverse () {}

    // 返回树中的最小节点
    min () {}

    // 返回树中的最大节点
    max () {}

    // 从树中移除一个节点
    remove (key) {}
}

插入节点

节点的顺序遵循从左节点到右节点左子节点上存储小（比父节点）的值，在右子节点上（比父节点）存储大（或等于）的值

insert(key) {
    const node = new Node(key);
    
    if(this.root === null) {
        this.root = node
    } else {
        
    }
}

查找节点

查找逻辑

如果树为空直接返回空
判断查询值于当前的树的根节点大小
如果小于节点进行节点左侧递归判断
如果大于节点进行节点右侧递归判断
相等就返回该节点

    search (key) {

       return this.searchNode(this.root, key)

    }

    searchNode(node, key) {
        if (node === null) return null;

        // 如果 查询元素 小于当前元素 左侧查询
        if (key < node.el) return this.searchNode(node.left, key);
        // 如果大于 右侧查询
        else if (key > node.el) return this.searchNode(node.right, key);
        else return node;
        
    }

中序遍历

遍历逻辑

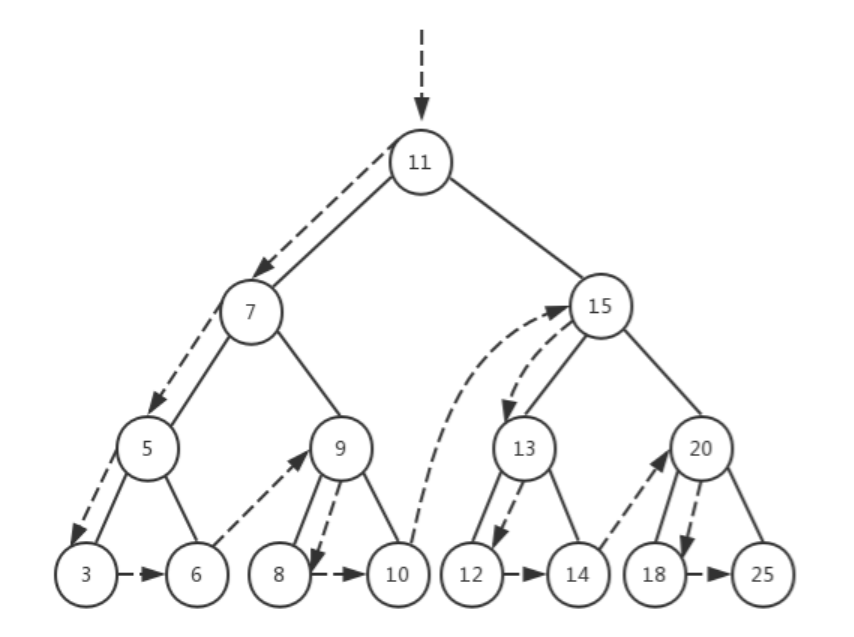
    inOrderTraverse (callback) {
        this.inOrderTraverseNode(this.root, callback)
    }

    inOrderTraverseNode (node, callback) {
        if (node !== null) {
            this.inOrderTraverseNode(node.left, callback);
            callback(node.el);
            this.inOrderTraverseNode(node.right, callback);
        }
    };

先序遍历

遍历规则

    preOrderTraverse (callback) {
        this.preOrderTraverseNode(this.root, callback)
    }

    preOrderTraverseNode (node, callback) {
        if (node !== null) {
            callback(node.el);
            this.preOrderTraverseNode(node.left, callback);
            this.preOrderTraverseNode(node.right, callback);
        }
    };

后序遍历

遍历规则

    postOrderTraverse (callback) {
        this.postOrderTraverseNode(this.root, callback)
    }

    postOrderTraverseNode (node, callback) {
        if (node !== null) {
            this.postOrderTraverseNode(node.left, callback);
            this.postOrderTraverseNode(node.right, callback);
            callback(node.el);

        }
    };

最小节点

最小节点永远都是树的最左侧节点

 if(this.root === null) return null;

        let node = this.root
        while (node.left) {
            node = node.left;
        }

        return node

最大节点

最大节点永远是最右侧的节点

 if(this.root === null) return null;

        let node = this.root
        while (node.right) {
            node = node.right;
        }

        return node

移除节点

remove (key) {
    if(this.root === null) return null;
    
}

树

二叉树​

二叉树的实现​

节点结构​

树结构​

插入节点​

查找节点​

中序遍历​

先序遍历​

后序遍历​

最小节点​

最大节点​

移除节点​

二叉树